Inverse trig functions are almost as bizarre as their functional counterparts. They tend to climb upward on the y-axis. Drop Patch L2 Interlude Pride on this page. They are funky because they need to be chopped into pieces in order to be considered functions. Remember that should yield only one y-value for each x-value.

To see how the sine and cosine functions are graphed, use a calculator, a computer, or a set of trigonometry tables to determine the values of the sine and cosi. Aug 20, 2007 - 8 min - Uploaded by Khan AcademyUsing the unit circle definition of the sine function to make a graph of it. To graph the sine function, we mark the angle along the horizontal x axis, and for each angle, we put the sine of that angle on the vertical y-axis. The result, as seen above, is a smooth curve that varies from +1 to -1. Curves that follow this shape are called 'sinusoidal' after the name of the sine function. This shape is also.

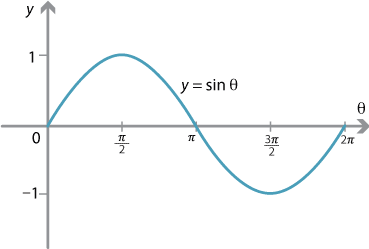
Otherwise, they won't pass the vertical line test. To graph the inverse sine function, we first need to limit or, more simply, pick a portion of our sine graph to work with.

Here's the graph of y = sin x. Next we limit the domain to [-90°, 90°]. In radians, that's [- π⁄ 2, π⁄ 2]. To find the inverse sine graph, we need to swap the variables: x becomes y, and y becomes x. Here's the graph of the inverse sine function, y = sin -1 x (or y = arcsin x): Inverse sine has a domain of [-1, 1] and a range of [- π⁄ 2, π⁄ 2].

See how the angles are on the y-axis this time, instead of on the x-axis like they were for the sine function? This means that when we're actually working problems using the inverse sine function, we'll be limited to Quadrant I and Quadrant IV (location is everything, as they say).